如图,在△ABC中,AB=CB,∠ABC=900,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.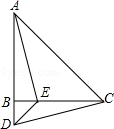
①求证:△ABE≌△CBD;
②若∠CAE=300,求∠BDC的度数.
在△ABC中, AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.△ABC的面积为:.
若△DEF三边的长分别为、2、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.


利用第2小题解题方法完成下题:如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.

无锡市南长区某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示.求日均销售量p(桶)与销售单价x(元)的函数关系;
若该经营部希望日均获利1350元,请你根据以上信息,就该桶装水的销售单价或销售数量,提出一个用一元二次方程解决的问题,并写出解答过程.

如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
若∠AOD =52º,求∠DEB的度数;
若OC=3,OA=5,求AB的长.
如图所示,A、B两个旅游点从2007年至2011年“五·一”的旅游人数变化情况分别用实线和虚线表示,根据图中所示解答以下问题:
B旅游点的旅游人数相对上一年,增长最快的是哪一年?
求A、B两个旅游点从2007到2011年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人,为控制游客数量,A旅游点决定提高门票价格.已知门票价格x (元)与游客人数y(万人)满足函数关系y=5-.若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少?
在平面直角坐标系内,A、B、C三点的坐标分别是A(5,0)、B(0,3)、C(5,3),O 为坐标原点,点E在线段BC上,若△AEO为等腰三角形, 求点E的坐标.(画出图象,不需要写计算过程)