(14分)已知椭圆的中心在原点O,焦点在坐标轴上,直线y = x +1与该椭圆相交于P和Q,且OP⊥OQ,|PQ|=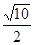 ,求椭圆的方程
,求椭圆的方程
(12分)函数 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、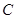 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形.
为正三角形.
(1)求 的值及函数
的值及函数 的值域;
的值域;
(2)若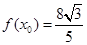 ,且
,且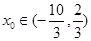 ,求
,求 的值.
的值.
已知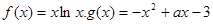
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数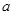 的取值范围.
的取值范围.
在△ABC中, 分别为内角A.B.C所对的边,且满足
分别为内角A.B.C所对的边,且满足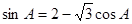
(1)求角A的大小
(2)现给出三个条件:① ②
②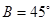 ③
③ 试从中选出两个可以确定△ABC的条件写出你的选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分)
试从中选出两个可以确定△ABC的条件写出你的选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分)
已知函数 .
.
(1)若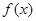 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若 是
是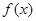 的极值点,求
的极值点,求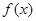 在
在 上的最小值和最大值.
上的最小值和最大值.
命题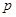 :关于
:关于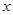 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数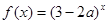 是增函数,若
是增函数,若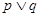 为真,
为真, 为假,求实数
为假,求实数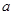 的取值范围.
的取值范围.