如图,平面直角坐标系中,⊙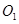 与
与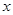 轴相切于点
轴相切于点 ,与
,与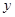 轴相交于点
轴相交于点 两点,连结
两点,连结 。
。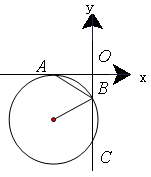
求证

若点
 的坐标为
的坐标为 ,直接写出点
,直接写出点 的坐标
的坐标在(2)的条件下,过
 两点作⊙
两点作⊙ 与
与 轴的正半轴交于点
轴的正半轴交于点 ,与
,与 的延长线交于点
的延长线交于点 ,当⊙
,当⊙ 的大小变化时,给出下列两个结论:
的大小变化时,给出下列两个结论:
①  的值不变;②
的值不变;② 的值不变;
的值不变;
其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值
先化简再求值: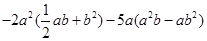 , 其中
, 其中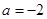 ,
,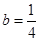 .
.
计算(每小题3分,共12分)
(1) ;
;
(2) ;
;
(3) ;
;
(4) .
.
(本题4分)(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M’处.请在正方形网格中画出△ABC平移后的图形△A’B’C’.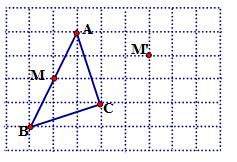
(2)若图中一小网格的边长为1,则△ABC的面积为_____.
如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(−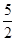 ,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
,k)是线段BC上一点,在线段BM上是否存在一点N,使直线PN平分△BCM的面积?若存在,请求出点N的坐标;若不存在,请说明理由.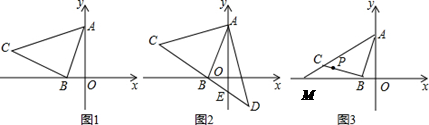
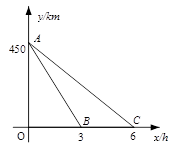
一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速
运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系,如图中线段AB所示.慢车离甲地的路
程y2(km)与行驶的时间x(h)之间的函数关系,如图中线段AC所示.根据图像进行以下研究.
解读信息:(1)甲、乙两地之间的距离为km;
(2)线段AB的解析式为;两车在慢车出发小时后相遇;
问题解决:
(3)设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数的图像.