化简
(1) ;
;
(2)
计算题
(1)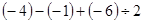
(2)
(3)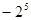
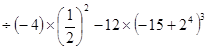
(4)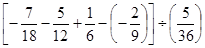
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形.
(1)已知某一勾股三角形的三个内角度数从小到大依次为x°、y°和z°,且xy=2160,求x+y的值;
(2)如图,△ABC是⊙O的内接三角形,AB= ,AC=
,AC= ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D.
①求证:△ABC是勾股三角形;
②求DE的长.
已知抛物线 (
( )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .直线
.直线 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,并且与直线
两点,并且与直线 相交于点
相交于点 .
.
(1)如图,将 沿
沿 轴翻折,若点
轴翻折,若点 的对应点
的对应点 ′恰好落在抛物线上,
′恰好落在抛物线上, ′与
′与 轴交于点
轴交于点 ,连结
,连结 ,求
,求 的值和四边形
的值和四边形 的面积;
的面积;
(2)在抛物线 (
( )上是否存在一点
)上是否存在一点 ,使得以
,使得以 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
小华早晨6点多钟去学校,去时看了一下手表,发现时针与分针的夹角为 度(0<
度(0< <180,
<180, 为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为
为整数),到了学校,他又看了一下手表,发现此时还不到7点钟,且时针与分针的夹角为也为 度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?
度,若小华去学校途中所用的时间是10的整数倍,那么,小华去学校途中所用的时间是多少?