(本小题满分12分)从2003年开始,我国就通过实施高校自主招生探索人才选拔制度改革,允许部分高校拿出一定比例的招生名额,选拔那些有特殊才能的学生。某学生参加一个高校的自主招生考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为 、
、 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为 ,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
(I)求该学生被学校录取的概率;
(II)设该学生答对题目的个数为ξ,求ξ的分布列和数学期望。
(本小题满分10分)【选修4-4:坐标系与参数方程】
已知曲线C的极坐标方程为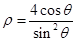 ,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,直线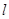 的参数方程为
的参数方程为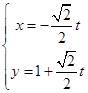 (t为参数).
(t为参数).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,把直线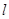 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求直线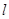 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
(本小题满分10分)【选修4-1:几何证明选讲】
如图,已知直线PA与圆O相切于点A,经过点O的割线PBC交圆O于点B和点C,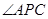 的平分线分别交AB,AC于点D和E.
的平分线分别交AB,AC于点D和E.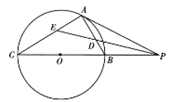
(Ⅰ)证明: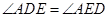 ;
;
(Ⅱ)若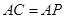 ,求
,求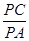 的值.
的值.
(本小题满分12分)在平面直角坐标系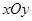 中,已知圆
中,已知圆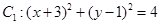 和圆
和圆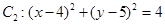 .
.
(Ⅰ)若直线 过点
过点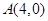 ,且被圆
,且被圆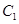 截得的弦长为
截得的弦长为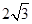 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线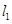 和
和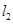 ,它们分别与圆
,它们分别与圆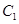 和圆
和圆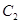 相交,且直线
相交,且直线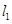 被圆
被圆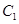 截得的弦长与直线
截得的弦长与直线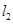 被圆
被圆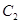 截得的弦长相等,试求所有条件的点P的坐标.
截得的弦长相等,试求所有条件的点P的坐标.
(本小题满分12分)已知函数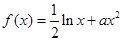
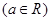 .
.
(Ⅰ)若曲线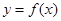 在点
在点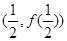 处的切线
处的切线 与直线
与直线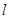 :
: 垂直,求a的值;
垂直,求a的值;
(Ⅱ)讨论函数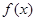 的单调性;若存在极值点
的单调性;若存在极值点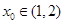 ,求实数a的取值范围.
,求实数a的取值范围.
如图,直三棱柱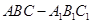 中,D、E分别是AB、
中,D、E分别是AB、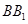 的中点.
的中点.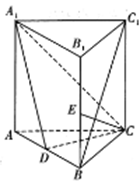
(Ⅰ)证明: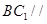 平面
平面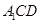 ;
;
(Ⅱ)设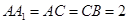 ,
,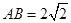 ,求四棱锥
,求四棱锥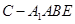 的体积.
的体积.