已知函数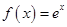 .
.
(1)设函数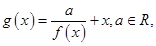 求
求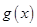 的极值.
的极值.
(2)证明: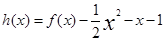 在
在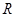 上为增函数。
上为增函数。
矩阵与变换: 已知a,b∈R,若 所对应的变换
所对应的变换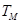 把直线
把直线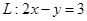 变换为自身,求实数
变换为自身,求实数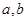 ,并求
,并求 的逆矩阵.
的逆矩阵.
已知函数 .
.
(1当 时,
时, 与
与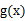 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的  的最小值。
的最小值。
(2)当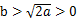 时,求证:存在
时,求证:存在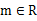 ,使
,使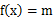 的三个不同的实数解
的三个不同的实数解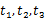 ,且对任意
,且对任意 且
且 都有
都有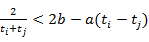 .
.
数列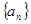 满足:
满足: ,
,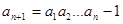 (
( ≥3),记
≥3),记
( ≥3).
≥3).
(1)求证数列 为等差数列,并求通项公式;
为等差数列,并求通项公式;
(2)设 ,数列{
,数列{ }的前n项和为
}的前n项和为 ,求证:
,求证: <
< <
< .
.
给定椭圆 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是 .
.
(1)若椭圆C上一动点 满足
满足 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为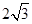 ,求P点的坐标;
,求P点的坐标;
(3)已知 ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点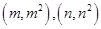 的直线的最短距离
的直线的最短距离 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
噪声污染已经成为影响人们身体健康和生活质量的严重问题.实践证明, 声音强度 (分贝)由公式
(分贝)由公式 (
( 为非零常数)给出,其中
为非零常数)给出,其中 为声音能量.
为声音能量.
(1)当声音强度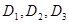 满足
满足 时,求对应的声音能量
时,求对应的声音能量 满足的等量关系式;
满足的等量关系式;
(2)当人们低声说话,声音能量为 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.