已知椭圆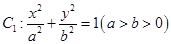 的离心率为
的离心率为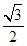 ,且经过点
,且经过点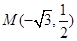 ,圆
,圆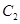 的直径为
的直径为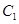 的长轴.如图,
的长轴.如图,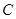 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点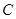 且与圆
且与圆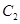 交于
交于 两点,
两点, 垂直于
垂直于 交椭圆于点
交椭圆于点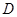 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
已知函数 .
.
(Ⅰ)当 时,求
时,求 的单调区间
的单调区间
(Ⅱ)若不等式 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数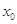 ,称
,称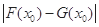 的值为两函数在
的值为两函数在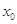 处的差值。证明:当
处的差值。证明:当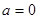 时,函数
时,函数 和
和 在其公共定义域内的所有差值都大干2.
在其公共定义域内的所有差值都大干2.
已知数列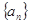 中,
中,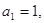 且点
且点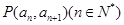 在直线
在直线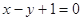 上。
上。
(1)求数列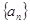 的通项公式;
的通项公式;
(2)若函数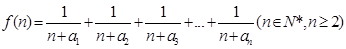 ,求函数
,求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前项和.试求出关于
的前项和.试求出关于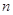 的整式
的整式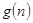 ,使得
,使得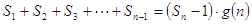 对于一切不小于2的自然数
对于一切不小于2的自然数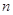 恒成立.(不用证明)
恒成立.(不用证明)
新一届中央领导集体非常重视勤俭节约,从“光盘行动”到“节约办春晚”。到饭店吃饭是吃光盘子或时打包带走,称为“光盘族”,否则称为“非光盘族”.政治课上政治老师选派几位同学组成研究性小组,从某社区[25,55]岁的人群中随机抽取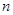 人进行了一次调查,得到如下统计表:
人进行了一次调查,得到如下统计表:
| 组数 |
分组 |
频数 |
频率 |
光盘族占本组比例 |
| 第1组 |
[25,30) |
50 |
0.05 |
30% |
| 第2组 |
[30,35) |
100 |
0.10 |
30% |
| 第3组 |
[35,40) |
150 |
0.15 |
40% |
| 第4组 |
[40,45) |
200 |
0.20 |
50% |
| 第5组 |
[45,50) |
a |
b |
65% |
| 第6组 |
[50,55) |
200 |
0.20 |
60% |
(1)求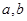 的值,并估计本社区[25,55)岁的人群中“光盘族”所占比例;
的值,并估计本社区[25,55)岁的人群中“光盘族”所占比例;
(2)从年龄段在[35,45)的“光盘族”中采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.求选取的2名领队分别来自[35,40)与[40,45)两个年龄段的概率。
在四棱锥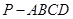 中,
中, 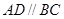 ,
,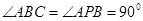 ,点
,点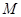 是线段
是线段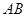 上的一点,且
上的一点,且 ,
,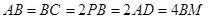 .
.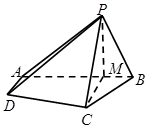
(1)证明:面 面
面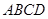 ;
;
(2)求直线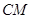 与平面
与平面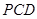 所成角的正弦值.
所成角的正弦值.
如图,海上有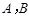 两个小岛相距10
两个小岛相距10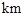 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为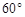 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至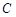 处进行作业,且
处进行作业,且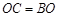 .设
.设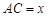
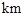 。
。
(1)若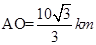 ,求出
,求出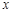 的取值;
的取值;
(2)用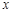 分别表示
分别表示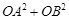 和
和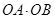 ,并求出
,并求出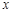 的取值范围.
的取值范围.