设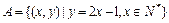 ,
, ,问是否存在非零整数
,问是否存在非零整数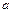 ,使
,使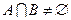 ?若存在,请求出
?若存在,请求出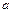 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
设离散型随机变量X的分布列为
| X |
0 |
1 |
2 |
3 |
4 |
| P |
0.2 |
0.1 |
0.1 |
0.3 |
m |
求:(Ⅰ)2X+1的分布列;
(Ⅱ)|X-1|的分布列.
已知P为曲线C上任一点,若P到点F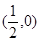 的距离与P到直线
的距离与P到直线 距离相等
距离相等
(1)求曲线C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点A、B,
(I)若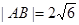 ,求直线l的方程;
,求直线l的方程;
(II)试问在x轴上是否存在定点E(a,0),使 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
已知函数
 .
.
(1)求 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.

(1)若 ,求
,求 ;
;
(2)若函数 对应的图象记为
对应的图象记为
(3)求曲线 在
在 处的切线方程?(II)若直线
处的切线方程?(II)若直线 为曲线
为曲线 的切线,并且直线
的切线,并且直线 与曲线
与曲线 有且仅有一个公共点,求所有这样直线
有且仅有一个公共点,求所有这样直线 的方程?
的方程?
已知在递增等差数列 中,
中, ,
, 成等比数列数列
成等比数列数列 的前n项和为Sn,且
的前n项和为Sn,且 .
.
(1)求数列 、
、 的通项公式;(2)设
的通项公式;(2)设 ,求数列
,求数列 的前
的前 和
和 .
.