已知:如图,二次函数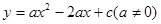 的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该二次函数的关系式;
(2)写出该二次函数的对称轴和顶点坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.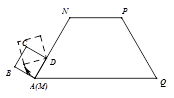
求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
(1) 如图,等腰直角△ABC的直角顶点B在直线l上,A、C在直线l的同侧.过A、C作直线l的垂线段AD、CE,垂足为D、E.请证明AD+CE=DE.
(2)如图,平面直角坐标系内的线段GH的两个端点的坐标为G(4,4),H(0,1).将线段GH绕点H顺时针旋转90°得到线段KH.求点K的坐标.
(3)平面直角坐标系内有两点P(a,b)、M(-3,2),将点P绕点M顺时针旋转90°得到点Q,请你直接写出点Q的坐标.
某企业在生产甲、乙两种节能产品时需用A、B两种原料,生产每吨节能产
品所需原料的数量如下表所示:由无锡市天一实验学校金杨建录制
| 原料 节能产品 |
A原料(吨) |
B原料(吨) |
| 甲种产品 |
3 |
3 |
| 乙种产品 |
1 |
5 |
销售甲、乙两种产品的利润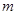 (万元)与销售量
(万元)与销售量 (吨)之间的函数关系如图所示.已知该企业生产了甲种产品
(吨)之间的函数关系如图所示.已知该企业生产了甲种产品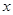 吨和乙种产品
吨和乙种产品 吨,共用去A原料200吨.
吨,共用去A原料200吨.
(1)写出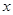 与
与 满足的关系式;
满足的关系式;
(2)为保证生产的这批甲种、乙种产品售后的总利润不少于220万元,那么至少要用B原料多少吨?
为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体
育成绩进行分段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下:
| 分数段 |
人数(人) |
频率 |
| A |
48 |
0.2 |
| B |
a |
0.25 |
| C |
84 |
0.35 |
| D |
36 |
b |
| E |
12 |
0.05 |
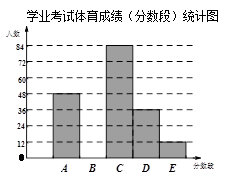
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为, b的值为,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内?(填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?