在直角坐标系 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 ,直线
,直线 与轨迹C交于A,B两点.
与轨迹C交于A,B两点.
(Ⅰ)写出轨迹C的方程; (Ⅱ)若

 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有| |>|
|>| |
|
(本小题满分12分)为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
(Ⅰ)求该校报考飞行员的总人数;
(Ⅱ)从这所学校报考飞行员的同学中任选一人,求这个人体重超过60公斤的概率.
(本小题满分12分)根据下列算法语句,将输出的A值依次记为

(Ⅰ)求数列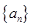 的通项公式;
的通项公式;
(Ⅱ)已知函数 的最小正周期是
的最小正周期是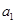 ,且函数
,且函数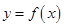 的图象关于直线
的图象关于直线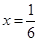 对称,求函数
对称,求函数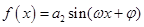 在区间
在区间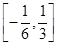 上的值域.
上的值域.
(本小题满分10分)(选修4—5,:不等式选讲)
(Ⅰ)证明柯西不等式: ;
;
(Ⅱ)若 且
且 ,用柯西不等式求
,用柯西不等式求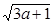 +
+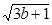 的最大值.
的最大值.
(本小题满分10分)选修4-4:坐标系与参数方程
将圆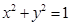 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与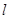 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(本小题满分10分)选修4-1:几何证明选讲.
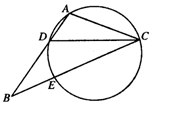
如图,在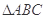 中,
中,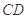 是
是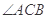 的角平分线,
的角平分线, 的外接圆交
的外接圆交 于点
于点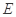 ,
,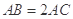 .
.
(Ⅰ)求证: ;
;
(Ⅱ)当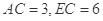 时,求
时,求 的长.
的长.