（本小题满分12分）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．
（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）从这所学校报考飞行员的同学中任选一人，求这个人体重超过60公斤的概率．
(本题满分15分) 已知直线l1：x＝my与抛物线C：y2＝4x交于O (坐标原点)，A两点，直线l2：x＝my＋m 与抛物线C交于B，D两
点．
(Ⅰ) 若 | BD | ＝ 2 | OA |，求实数m的值；
(Ⅱ) 过A，B，D分别作y轴的垂线，垂足分别为A1，B1，D1．记S1，S2分别为三角形OAA1和四
边形BB1D1D的面积，求
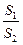的取值范围．
(本题满分15分) 已知实数a满足1＜a≤2，设函数f (x)＝
x3－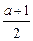
x2＋ax．
(Ⅰ) 当a＝2时，求f (x)的极小值；
(Ⅱ) 若函数g(x)＝4x3＋3bx2－6(b＋2)x (b∈R) 的极小值点与f (x)的极小值点相同，
求证：g(x)的极大值小于等于10．
(本题满分14分) 如图，在三棱柱BCD－B1C1D1与四棱锥A－BB1D1D的组合体中，已知BB1⊥平面BCD，四边形ABCD是平行四边形，∠ABC＝120°，AB＝
，AD＝3，BB1＝1．
(Ⅰ) 设O是线段BD的中点，
求证：C1O∥平面AB1D1；
(Ⅱ) 求直线AB1与平面ADD1所成的角．
(本题满分14分) 设首项为a1，公差为d的等差数列{an}的前n项和为Sn．
已知a7＝－2，S5＝30．
(Ⅰ) 求a1及d；
(Ⅱ) 若数列{bn}满足an＝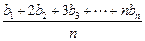
(n∈N*)，
求数列{bn}的通项公式
．
(本题满分14分)在锐角△ABC中，cos B＋cos (A－C)＝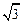
sin C．
(Ⅰ) 求角A的大小；
(Ⅱ) 当BC＝2时，求△ABC面积的最大值．