(本小题满分10分)选修4-4:坐标系与参数方程
将圆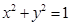 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与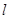 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
如图,在直三棱柱ABCA1B1C1中,已知∠ACB=90°,M为A1B与AB1的交点,N为棱B1C1的中点.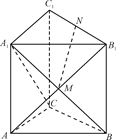
(1)求证:MN∥平面AA1C1C;
(2)若AC=AA1,求证:MN⊥平面A1BC.
如图,在锥体PABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=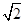 ,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
由平面α外一点P引平面的三条相等的斜线段,斜足分别为A、B、C,O为△ABC的外心,求证:OP⊥α.
在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.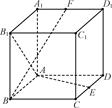
(1)求证:AB1⊥BF;
(2)求证:AE⊥BF;
(3)棱CC1上是否存在点F,使BF⊥平面AEP,若存在,确定点P的位置;若不存在,说明理由.
在正三棱柱ABCA1B1C1中,点D是BC的中点,BC=BB1.
(1)若P是CC1上任一点,求证:AP不可能与平面BCC1B1垂直;
(2)试在棱CC1上找一点M,使MB⊥AB1.