某大学举办“我爱记歌词”校园歌手大赛,经过层层选拔,有5人进入决赛,决赛办法如下:选手参加“千首电脑选歌”演唱测试,测试过关者即被授予“校园歌手”称号,否则参加“百首电脑选歌”演唱测试。若“百首电脑选歌”测试过关也被授予“校园歌手”称号,否则被彻底淘汰。若进入决赛的5人“千首电脑选歌”演唱测试过关的概率是0.5,“百首电脑选歌”演唱测试合格的概率是0.8,而且每个人每轮测试是否合格是相互独立的,试计算(结果精确到0.01)
(1)恰好有两人参加“百首电脑选歌”演唱的概率;
(2)平均有几人参加“百首电脑选歌”演唱(保留小数);
(3)至少一人被最终淘汰的概率。
如图,过点P(1,0)作曲线C: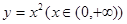 的切线,切点为
的切线,切点为 ,设点
,设点 在
在 轴上的投影是点
轴上的投影是点 ;又过点
;又过点 作曲线
作曲线 的切线,切点为
的切线,切点为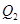 ,设
,设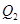 在
在 轴上的投影是
轴上的投影是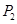 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点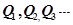
 ,设点
,设点 的横坐标为
的横坐标为 .
.
(1)求直线 的方程;
的方程;
(2)求数列 的通项公式;
的通项公式;
(3)记 到直线
到直线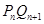 的距离为
的距离为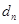 ,求证:
,求证: 时,
时,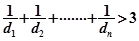
如图甲,在平面四边形ABCD中,已知
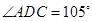 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.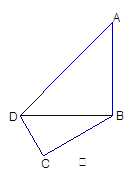
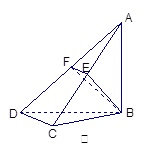
(1)求证:DC 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
甲、乙两人在罚球线互不影响地投球,命中的概率分别为 与
与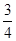 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(1)甲、乙两人在罚球线各投球一次,求两人得分之和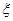 的数学期望;
的数学期望;
(2)甲、乙两人在罚球线各投球二次,求甲恰好比乙多得分的概率.
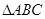 的三个内角
的三个内角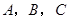 对应的三条边长分别是
对应的三条边长分别是 ,且满足
,且满足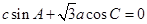
(1)求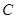 的值;
的值;
(2)若 ,
, 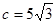 ,求
,求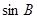 和
和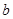 的值.
的值.
已知定义在实数集上的函数 ,
, ,其导函数记为
,其导函数记为 ,
,
(1)设函数 ,求
,求 的极大值与极小值;
的极大值与极小值;
(2)试求关于 的方程
的方程 在区间
在区间 上的实数根的个数。
上的实数根的个数。