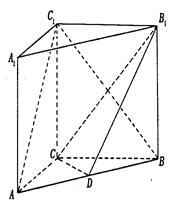
如图甲,在平面四边形ABCD中,已知
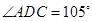 ,
, ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.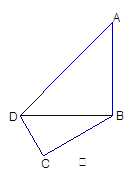
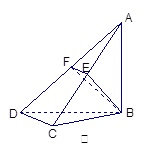
(1)求证:DC 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
甲袋中装有大小相同的红球1个,白球2个;乙袋中装有与甲袋中相同大小的红球2个,白球3个.先从甲袋中取出1个球投入乙袋中,然后从乙袋中取出2个小球.
(Ⅰ)求从乙袋中取出的2个小球中仅有1个红球的概率;
(Ⅱ)记从乙袋中取出的2个小球中白球个数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
△ABC中,角A、B、C对边分别是a、b、c,满足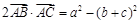 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求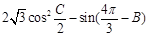 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
设椭圆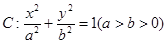 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且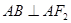 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过 三点的圆恰好与直线
三点的圆恰好与直线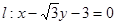 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点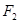 作斜率为
作斜率为
 的直线
的直线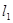 与椭圆
与椭圆 交于
交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点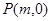 使得
使得 ,如果存在,求出
,如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
已知函数
(1)求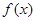 的单调减区间;
的单调减区间;
(2)若方程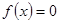 有三个不同的实根,求
有三个不同的实根,求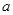 的取值范围;
的取值范围;
(3)若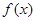 在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
如图, 在直三棱柱 中,
中,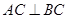 ,
,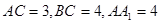 ,点
,点 是
是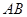 的中点,
的中点,
(1)求证: ;
;
(2)求证: ;
;
(3)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.