设椭圆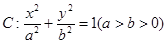 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且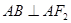 .
.
(1)求椭圆 的离心率;
的离心率;
(2)若过 三点的圆恰好与直线
三点的圆恰好与直线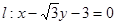 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点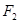 作斜率为
作斜率为
 的直线
的直线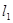 与椭圆
与椭圆 交于
交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点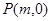 使得
使得 ,如果存在,求出
,如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
已知函数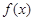 是定义在
是定义在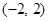 上的奇函数且是减函数,若
上的奇函数且是减函数,若 ,求实数
,求实数 的取值范围。
的取值范围。
已知f(x)=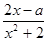 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)=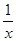 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
已知,椭圆C以过点A(1, ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
求椭圆C的方程;
E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
设函数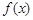 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=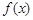 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(1)求a,b的值;
(2)证明: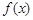 ≤2x-2.
≤2x-2.
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| 男 |
女 |
总计 |
|
| 爱好 |
40 |
||
| 不爱好 |
30 |
||
| 总计 |
(2)通过计算说明,是否有99%以上的把握认为“爱好该项运动与性别有关”?参考信息如下:
 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
