某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
|
|
| 不爱好 |
|
30 |
|
| 总计 |
|
|
|
(2)通过计算说明,是否有99%以上的把握认为“爱好该项运动与性别有关”? 参考信息如下:
 |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |

一个口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试用概率说明理由.
如图,已知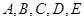 均在⊙O上,且
均在⊙O上,且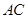 为⊙O的直径。
为⊙O的直径。
(1)求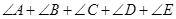 的值;
的值;
(2)若⊙O的半径为 ,
, 与
与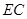 交于点
交于点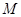 ,且
,且 、
、 为弧
为弧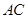 的三等分点,求
的三等分点,求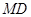 的长.
的长.
已知函数 ,
,
(Ⅰ)若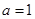 ,求函数
,求函数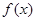 的极值;
的极值;
(Ⅱ)设函数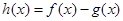 ,求函数
,求函数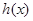 的单调区间;
的单调区间;
(Ⅲ)若在区间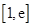 (
(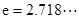 )上存在一点
)上存在一点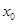 ,使得
,使得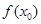
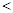
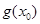 成立,求
成立,求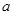 的取值范围.
的取值范围.
已知椭圆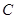 的焦点在
的焦点在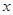 轴上,离心率
轴上,离心率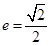 ,且经过点
,且经过点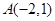 .
.
(Ⅰ)求椭圆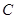 的标准方程;
的标准方程;
(Ⅱ)斜率为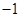 的直线
的直线 与椭圆
与椭圆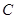 相交于
相交于 两点,求证:直线
两点,求证:直线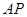 与
与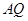 的倾斜角互补.
的倾斜角互补.
四棱锥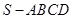 中,底面
中,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 ,
,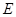 为
为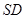 的中点,已知
的中点,已知 ,
,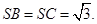

(Ⅰ)求证: ;
;
(Ⅱ)在 上求一点
上求一点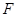 ,使
,使 平面
平面 ;
;
(Ⅲ)求三棱锥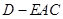 的体积.
的体积.