已知函数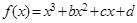 的图象过点
的图象过点 ,且在点
,且在点 处的切线方程为
处的切线方程为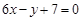 .
.
(1)求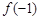 和
和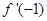 的值;
的值;
(2)求函数 的解析式.
的解析式.
设抛物线y2=4x截直线y=2x+k所得弦长|AB|=3 .
.
(1)求k的值;
(2)以弦AB为底边,x轴上的P点为顶点组成的三角形面积为39时,求点P的坐标.
已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和M的值.
设数列 的前
的前 项和为
项和为 ,若对所有正整数
,若对所有正整数 ,都有
,都有 .
.
证明 是等差数列.
是等差数列.
设椭圆 (a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA= (O为原点),求椭圆离心率的取值范围.
(O为原点),求椭圆离心率的取值范围.
如图,A、B、C是三个观察哨,A在B的正东,两地相距6 kM,C在B的北偏西30°,两地相距4 kM.在某一时刻,A观察哨发现某种信号,并知道该信号的传播速度为1 kM/s;4秒后B、C两个观察哨同时发现这种信号.在以过A、B两点的直线为x轴,以线段AB的垂直平分线为y轴的直角坐标系中,指出发射这种信号的地点P的坐标.