如图,A、B、C是三个观察哨,A在B的正东,两地相距6 kM,C在B的北偏西30°,两地相距4 kM.在某一时刻,A观察哨发现某种信号,并知道该信号的传播速度为1 kM/s;4秒后B、C两个观察哨同时发现这种信号.在以过A、B两点的直线为x轴,以线段AB的垂直平分线为y轴的直角坐标系中,指出发射这种信号的地点P的坐标.
经过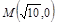 作直线
作直线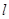 交曲线
交曲线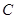 :
: (
(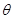 为参数)于
为参数)于 、
、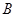 两点,若
两点,若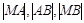 成等比数列,求直线
成等比数列,求直线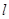 的方程.
的方程.
( 12分)如图,在四棱锥 中,侧面
中,侧面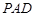 是正三角形,底面
是正三角形,底面 是边长为2的正方形,侧面
是边长为2的正方形,侧面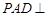 平面
平面 为
为 的中点.
的中点.
①求证: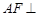 平面
平面 ;
;
②求直线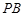 与平面
与平面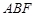 所成角的正切值.
所成角的正切值.
在 中,角
中,角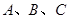 的对边分别为
的对边分别为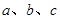 ,且
,且 .
.
①求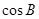 的值;
的值;
②若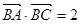 ,且
,且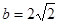 ,求
,求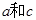 的值.
的值.
.某企业为考察生产同一种产品的甲、乙两条生产线的产品合格率,同时各抽取100件产品,检验后得到如下列联表:
生产线与产品合格数列联表
| 合格 |
不合格 |
总计 |
|
| 甲线 |
97 |
3 |
100 |
| 乙线 |
95 |
5 |
100 |
| 总计 |
192 |
8 |
200 |
请问甲、乙两线生产的产品合格率在多大程度上有关系?
在回归分析中,通过模型由解释变量计算预报变量的值时,应注意什么问题?