已知二次函数y=ax2+2x+c，函数y与自变量x的部分对应值如下表：
| x |
…… |
－2 |
－1 |
0 |
1 |
2 |
…… |
| y |
…… |
－5 |
0 |
3 |
4 |
3 |
…… |
求这个二次函数的关系式；
请判断函数有最大值还是最小值，并写出此时x的值与y的值；
若y≥0，则x的取值范围是_______．
若A(n，y1)、B(n+1，y2)两点均在该函数的图象上，试比较y1与y2大小．
如图，在平面直角坐标系xOy中，矩形OEFG的顶点E坐标为（4，0），顶点G坐标为（0，2）．将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．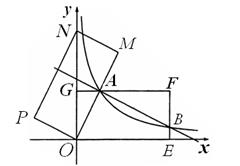
（1）判断△OGA和△NPO是否相似，并说明理由；
（2）求过点A的反比例函数解析式；
（3）若（2）中求出的反比例函数的图象与EF交于B点，请探索：直线AB与OM是否垂直，并说明理由．
（本题10分）我校八年级举行英语风采演讲比赛，派两位老师去超市购买笔记本作为奖品．据了解，该超市的甲、乙两种笔记本的价格分别是10元和6元，他们准备购买这两种笔记本共30本．
（1）若这两位老师计划用220元购买奖品，则能买这两种笔记本各多少本?
（2） 若他们根据演讲比赛的设奖情况，决定所购买的甲种笔记本的数量不多于乙种笔记本数量的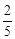
，但又多于乙种笔记本数量的
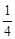，若设他们买甲种笔记本x本，买这两种笔记本共花费y元．
①求出y（元）关于x（本）的函数关系式；
②问购买这两种笔记本各多少时，花费最少，此时的花费是多少元？
如图，已知
的中垂线
交
于点
，交
于点
，有下面3个结论：
①
是等腰三角形；
②
∽
；
③点D是线段AC的黄金分割点．
请你从以上结论中只选一个加以证明
（友情提醒：证明①得8分，证明②得10分，证明③得12分）．
如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数
的图象的两个交点．
（1） 求此反比例函数的解析式及n的值；
（2） 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
小美有红色、白色、蓝色上衣各一件，黄色、黑色长裤各一条．
（1）请用画树状图或列表的方法分析小美上衣和长裤有多少种不同的搭配情况；
（2）其中小美穿蓝色上衣的概率是多少？