(1)计算: (2)化简
(2)化简 .
.
如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为(0,2),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C为y轴正半轴上一点,且OC=AB,抛物线y= x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.
(1)求此抛物线的函数表达式;
(2)求证:∠BEF=∠AOE;
(3)当△EOF为等腰三角形时,求此时点E的坐标;
(4)在(3)的条件下,当直线EF交x轴于点D,P为(1)中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的( )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
某公司开发了一种新型的家电产品,又适逢“家电下乡”的优惠政策.现投资40万元用于该产品的广告促销,已知该产品的本地销售量y1(万台)与本地的广告费用x(万元)之间的函数关系满足 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.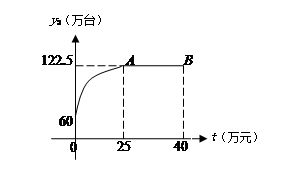
(1)结合图象,写出y2(万台)与外地广告费用t(万元)之间的函数关系式;
(2)求该产品的销售总量y(万台)与外地广告费用t(万元)之间的函数关系式;
(3)如何安排广告费用才能使销售总量最大?
综合实践课上,小明所在小组要测量护城河的宽度.如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 
如图,在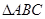 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的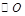 交BC于点M,
交BC于点M,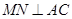 于点N.
于点N.
(1)求证:MN是⊙O的切线;
(2)若 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.