如图四棱锥 ,底面四边形ABCD满足条件
,底面四边形ABCD满足条件 ,
, ,侧面SAD垂直于底面ABCD,
,侧面SAD垂直于底面ABCD, ,
,
(1)若SB上存在一点E,使得 平面SAD,求
平面SAD,求 的值;
的值;
(2)求此四棱锥体积的最大值;
(3)当体积最大时,求二面角A-SC-B大小的余弦值.
(本小题满分12分)
若函数 为奇函数,当
为奇函数,当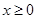 时,
时,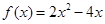 (如图).
(如图).
(1)请补全函数 的图象;(2)写出函数
的图象;(2)写出函数 的表达式;
的表达式;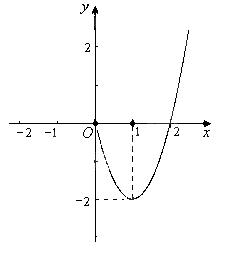
(3)用定义证明函数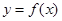 在区间
在区间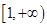 上单调递增
上单调递增
.(本小题满分10分)
已知 ,
, 是一次函数,并且点
是一次函数,并且点 在函数
在函数 的图象上,点
的图象上,点 在函数
在函数 的图象上,求
的图象上,求 的解析式
的解析式
(本小题14分)已知函数f(x)=ax3+bx2+cx是R上的奇函数,且f(1)=2,f(2)=10
(1)确定函数 的解析式;(2)用定义证明
的解析式;(2)用定义证明 在R上是增函数;
在R上是增函数;
(3)若关于x的不等式f(x2-4)+f(kx+2k)<0在x∈(0,1)上恒成立,求k的取值范围。
(本小题12分)已知圆C满足(1)截y轴所得弦MN长为4;(2)被x轴分成两段圆弧,其弧 长之比为3:1,且圆心在直线y=x上,求圆C的方程。
(为方便学生解答,做了一种情形的辅助图形)
(本小题12分)已知空间四边形ABCD中,AC=AD,BC=BD,且E是CD的中点,F是BD的中点, (1)求证:BC∥平面AFE(2)平面ABE⊥平面ACD