已知平面上的动点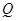 到定点
到定点 的距离与它到定直线
的距离与它到定直线 的距离相等
的距离相等
(1)求动点 的轨迹
的轨迹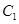 的方程
的方程
(2)过点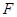 作直线
作直线 交
交 于
于 两点(
两点( 在第一象限),若
在第一象限),若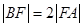 ,求直线
,求直线 的方程
的方程
(3)试问在曲线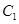 上是否存在一点
上是否存在一点 ,过点
,过点 作曲线
作曲线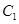 的切线
的切线 交抛物线
交抛物线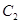 于
于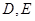 两点,使得
两点,使得 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
已知中心在原点,对称轴为坐标轴的双曲线的一个焦点为
且该双曲线上一点到两个焦点的距离差的绝对值为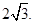
(Ⅰ)求双曲线的标准方程.
(Ⅱ)过点 且倾斜角为
且倾斜角为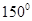 的直线与双曲线交于
的直线与双曲线交于 两点,求线段
两点,求线段 的长。
的长。
如图,在正三棱柱 中,
中, 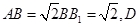 为
为 的中点。
的中点。
(Ⅰ)求证: 平面
平面 ;(Ⅱ)求直线
;(Ⅱ)求直线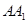 与平面
与平面 所成角的正弦值
所成角的正弦值
如图,在四棱锥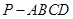 中,底面
中,底面 为正方形,侧棱
为正方形,侧棱 底面
底面 ,
, ,点
,点 为
为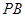 的中点。
的中点。
(Ⅰ)求证: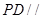 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面 的距离。
的距离。
已知圆C的圆心在直线 上且在第一象限,圆C与
上且在第一象限,圆C与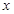 相切, 且被直线
相切, 且被直线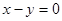 截得的弦长为
截得的弦长为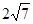 .
.
(1)求圆C的方程;
(2)若 是圆C上的点,满足
是圆C上的点,满足 恒成立,求
恒成立,求 的范围.
的范围.
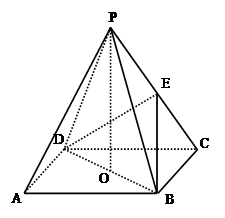
如图,ABCD是正方形,O是正方形的中心, PO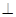 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:(1)PA∥平面BDE;
(2)平面PAC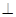 平面BDE
平面BDE