已知中心在原点,对称轴为坐标轴的双曲线的一个焦点为
且该双曲线上一点到两个焦点的距离差的绝对值为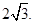
(Ⅰ)求双曲线的标准方程.
(Ⅱ)过点 且倾斜角为
且倾斜角为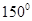 的直线与双曲线交于
的直线与双曲线交于 两点,求线段
两点,求线段 的长。
的长。
已知抛物线 的焦点为
的焦点为 ,直线
,直线 与
与 轴的交点为
轴的交点为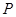 ,与抛物线
,与抛物线 的交点为
的交点为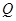 ,且
,且 .已知椭圆
.已知椭圆
 的右焦点
的右焦点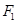 与抛物线
与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .
.
(1)求抛物线 和椭圆
和椭圆 的方程;
的方程;
(2)若过椭圆 的右焦点
的右焦点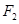 的直线
的直线 与椭圆交于
与椭圆交于 、
、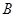 两点,求三角形
两点,求三角形 (
( 为坐标原点)的面积
为坐标原点)的面积 的最大值.
的最大值.
如图1,在 中,
中, ,
, ,
, 是
是 上的高,沿
上的高,沿 将
将 折成
折成 的二面角
的二面角 ,如图2.
,如图2.
(1)证明:平面
 平面
平面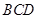 ;
;
(2)设 为
为 的中点,
的中点, ,求异面直线
,求异面直线 与
与 所成的角的大小.
所成的角的大小.
设数列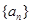 的前
的前 项和为
项和为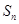 ,已知
,已知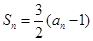 .
.
(1)求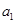 的值,并求数列
的值,并求数列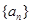 的通项公式;
的通项公式;
(2)若数列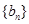 为等差数列,且
为等差数列,且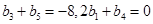 .设
.设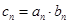 ,数列
,数列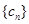 的前
的前 项和为
项和为 .
.
证明:对任意 ,
, 是一个与
是一个与 无关的常数.
无关的常数.
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)将函数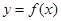 的图象向下平移
的图象向下平移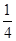 个单位,再将图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
个单位,再将图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到函数 的图象,求使
的图象,求使 成立的
成立的 的取值集合.
的取值集合.
在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:
| 感染 |
未感染 |
总计 |
|
| 服用 |
10 |
40 |
50 |
| 未服用 |
20 |
30 |
50 |
| 总计 |
30 |
70 |
100 |
附表:
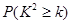 |
0.10 |
0.05 |
0.025 |
 |
2.706 |
3.841 |
5.024 |
参照附表,在犯错误的概率不超过(填百分比)的前提下,认为“小动物是否被感染与有没有服用疫苗有关” .