在西非肆虐的“埃博拉病毒”的传播速度很快，这已经成为全球性的威胁．为了考察某种埃博拉病毒疫苗的效果，现随机抽取100只小鼠进行试验，得到如下列联表：
| |
感 染 |
未感染 |
总 计 |
| 服用 |
10 |
40 |
50 |
| 未服用 |
20 |
30 |
50 |
| 总计 |
30 |
70 |
100 |
附表：
 |
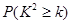0．10 |
0．05 |
0．025 |
 |
2．706 |
3．841 |
5．024 |
参照附表，在犯错误的概率不超过（填百分比）的前提下，认为“小动物是否被感染与有没有服用疫苗有关” ．
在
中，满足
的夹角为
，
是
的中点，
（1）若
，求向量
的夹角的余弦值；.
（2）若
，点
在边
上且
，如果
，求
的值。
已知函数
的定义域为
，
（1）求；
（2）若
，且是
的真子集，求实数
的取值范围.
已知函数
．
（1）当
时，求函数
的定义域；
（2）若关于
的不等式
的解集是
，求
的取值范围．
在直角坐标系
中，曲线C的参数方程为
为参数），曲线P在以该直角坐标系的原点O的为极点，x轴的正半轴为极轴的极坐标系下的方程为
.
（1）求曲线C的普通方程和曲线P的直角坐标方程；
（2）设曲线C和曲线P的交点为A、B，求|AB|.
已知函数
（
）．
（1）求
的单调区间；
（2）如果
是曲线
上的任意一点，若以为切点的切线的斜率
恒成立，求实数
的最小值；
（3）讨论关于
的方程
的实根情况．