某车间有２０名工人，每人每天可加工甲种零件５件或乙种零件４件。在这２０名工人中，派ｘ人加工乙种零件，其余的加工甲种零件，已知每加工一个甲种零件可获利１６元，每加工一个乙种零件可获利２４元，若要使车间每天获利不低于１８００元，写出x所要满足的不等关系．
有时可用函数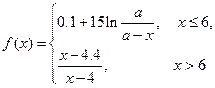
述学习某学科知识的掌握程度．其中
表示某学科知识的学习次数（
），
表示对该学科知识的掌握程度，正实数a与学科知识有关
（1）证明：当x 
7时，掌握程度的增长量f（x+1）- f（x）总是下降；
（2）根据经验，学科甲、乙、丙对应的a的取值区间分别为（115，121］,（12
1,127］
（127,133］．当学习某学科知识6次时，掌握程度是
85%，请
确定相应的学科．
某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售
量可以增加，且每星期多卖出的商品件数与商品单价的降低值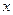
（单位：元，
）
的平方成正比，已知商品单价降低2元时，一星期多卖出24件．
（I）将一个星期的商品销售利润表示成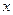的函数；
（II）如何定价才能使一个星期的商品销售利润最大？
(本小题满分12分）
已知函数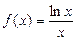
的图象为曲线
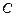, 函数
的图象为直线
.
(Ⅰ) 当
时, 求
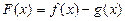的最大值;
(Ⅱ) 设直线与曲线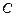的交点的横坐标分别为
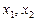, 且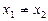
,
求证: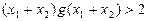 
.
(本小题满分12分）已知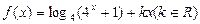函数
为偶函数.
(Ⅰ) 求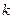
的值;
(Ⅱ) 若方程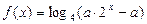
有且只有一个根, 求实数
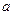的取值范围.