如图所示，一个竖直放置的圆锥筒可绕其中心轴OO′转动，筒内壁粗糙，筒口半径和筒高分别为R和H，筒内壁A点的高度为筒高的一半．内壁上有一质量为m的小物块．
当筒不转动时，物块静止在筒壁A点受到的摩擦力大小为 ；支持力的大小为 。
当物块在A点随筒做匀速转动，且其所受到的摩擦力为零时，筒转动的角速度的大小为
。
指出下面四个图中电场线(或等势面)画法有哪些错误．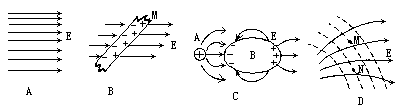
| A．电场线相互平行，但分布不均匀,_______________________ ______________________________________________________; |
| B．M为放置在匀强电场E中的金属板_______________________ ______________________________________________________. |
| C．B为静电平衡时的感应导体_____________________________ ______________________________________________________. |
D．虚线所示为电势差相等的几个等势面，且 ________ |
______________________________________________________.
如图1－2－14所示质量为m＝60kg的人站在质量为M＝30kg的木板上，人和木板之间的动摩擦因数为0.4,木板和水平地面的动摩擦因数为0.2，今人用绕过定滑轮的绳子拉木板使木板和他自己一起向右作匀速直线运动，那么，木板一共受个力的作用；人和木板之间的摩擦力为N．
如图所示，一根细长的轻弹簧系着一个小球，弹簧的另一端固定在天花板上，静止时，小球处于位置O，现手握小球把弹簧拉长，放手后小球便在竖直方向上下来回运动，B、C分别为小球到达的最低点和最高点，小球向上经过位置O时开始计时，其经过各点的时刻如图所示，若测得OB＝OC＝10cm，AB＝3cm，则自0时刻开始。
(1) 0.2s内小球发生的位移大小是 ，方向 ，经过的路程是 。
(2) 0.5s内小球发生的位移大小是 ，方向 ，经过的路程是 。
(3) 0.8s内小球发生的位移大小是 ，方向 ，经过的路程是 。
一质点绕半径为R的圆周运动了一圈，则其位移大小为，路程是。若质点运动了
周，则其位移大小为，路程是，运动过程中最大位移是最大路程是。
科学实验是人们认识自然的重要手段．一学生测量自行车在行驶中所受的阻力系数k(阻力对重力的比值)，他依次做了以下事项：(1)找一段平直的路面，并在路面上画一道起点线；(2)以较大速度骑车驶过起点线，并在通过起点线时按动秒表开始计时；(3)当车驶过起点线后就不再蹬车，让自行车依靠惯性沿直线继续前进；(4)自行车停下，立即按下秒表停止计时，记录自行车行驶时间t，同时记下终点位置；(5)量出起点线到终点的距离L．根据上述操作，可测出自行车在行驶中的阻力系数k=. 