如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间.
如图,A、D、B、C是⊙O上的四点,∠ ADC=∠CDB=60°,判断ABC的形状并证明你的结论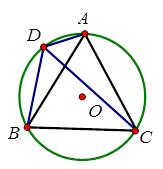
已知二次函数 的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围
如图,在平面直角坐标系中,四边形ABCD的四个顶点的坐标分别是A(1,3)、
B(2,2)、C(2,1),D(3,3).
(1)以原点O为位似中心,相似比为2,将图形放大,画出符合要求的位似四边形;
(2)在(1)的前提下,写出点A的对应点坐标A′
如图10-1,在平面直角坐标系 中,点
中,点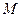 在
在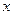 轴的正半轴上, ⊙
轴的正半轴上, ⊙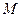 交
交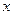 轴于
轴于  两点,交
两点,交 轴于
轴于 两点,且
两点,且 为
为 的中点,
的中点,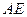 交
交 轴于
轴于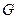 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),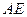


(1)(3分)求点 的坐标.
的坐标.
(2)(3分)连结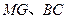 ,求证:
,求证: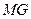 ∥
∥
(3)(4分) 如图10-2,过点 作⊙
作⊙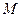 的切线,交
的切线,交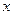 轴于点
轴于点 .动点
.动点 在⊙
在⊙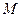 的圆周上运动时,
的圆周上运动时, 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
如图9,抛物线 与
与 轴交于
轴交于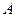 、
、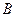 两点(点
两点(点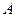 在点
在点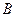 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点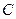 在第一象限,满足∠
在第一象限,满足∠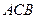 为直角,且恰使△
为直角,且恰使△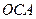 ∽△
∽△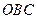 .
.
(1)(3分)求线段 的长.
的长.
(2)(3分)求该抛物线的函数关系式.
(3)(4分)在 轴上是否存在点
轴上是否存在点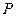 ,使△
,使△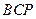 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的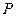 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.