已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
育才中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:
(1)样本的容量是多少?
(2)在如图2中,将“体育”部分的图形补充完整.
(3)试确定图1中,“音乐”部分所对应的圆心角的大小.
(4)估计育才中学现有的学生中,有多少人爱好“书画”?
联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某实验中学课外活动小组对全校师生开展了“爱好环境,从我做起”为主题的问卷调查,并将调查结果分析整理后完成了下面的两个统计图.
其中:
| A.能将垃圾放到规定的地方,而且还会考虑垃圾的分类; |
| B.能将垃圾放到规定的地方,但不会考虑垃圾的分类; |
| C.偶尔将垃圾放在规定的地方; |
| D.随手乱扔垃圾. |
根据以上信息回答下列问题: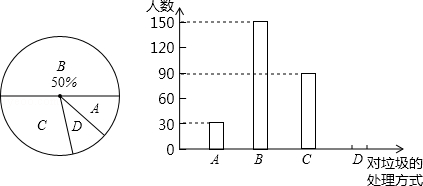
(1)该校课外活动小组共调查了多少人?并补全条形统计图;
(2)如果该校共有师生3060人,那么随手乱扔垃圾的约有多少人?
丹东市政府决定,从2011年起在全市开展创建全国文明城市,国家卫生城市,国家环保模范城市,国家园林城市“四城联创”活动.小东同学在全校随机调查了若干名学生对“四城联创”的了解程度,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:
(1)在这次调查活动中,一共调查了多少名学生;
(2)在条形统计图中,将表示B、D的部分补充完整;
(3)在扇形统计图中,计算出C部分所对应的圆心角的度数;
(4)若该校有学生1200名,估计对“四城联创”了解程度为“熟悉”的学生约有多少名?
某商场对今年“家电下乡”A、B、C三种品牌的电视机在第四季度销售情况进行统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:
(1)这个商场第四季度共销售电视机多少台?
(2)补全条形统计图;
(3)写出B品牌电视机在图中所对应的圆心角的度数;
(4)根据上述统计信息,2010年第一季度该商场如何进货?请你提一条合理化的建议.
下表是某网站向社会公众开展的对明年房价走势的调查数据统计表:
| 看法 |
人数 |
| A 房价要降 |
3335 |
| B 房价持平 |
2001 |
| C 房价要涨 |
1201 |
| D 无法预测 |
133 |
(1)根据表制作出条形统计图.
(2)根据表制作出扇形统计图.