（本小题满分15分） 已知抛物线C的顶点在原点， 焦点为F(0，1).
（1） 求抛物线C的方程；
（2）在抛物线C上是否存在点P， 使得过点P
的直线交C于另一点Q，满足PF⊥QF， 且
PQ与C在点P处的切线垂直.若存在，求出
点P的坐标； 若不存在，请说明理由.
有编号为
,
,…
的10个零件，测量其直径（单位：cm），得到下面数据：
其中直径在区间[1.48，1.52]内的零件为一等品。
（Ⅰ）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；
（Ⅱ）从一等品零件中，随机抽取2个.
（ⅰ）用零件的编号列出所有可能的抽取结果；
（ⅱ）求这2个零件直径相等的概率。
（本小题满分12分）
在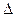
ABC中，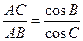
。
（Ⅰ）证明B=C：
（Ⅱ）若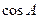
=-
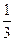，求sin
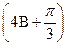的值。
已知椭圆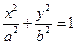
（a>b>0）的离心率e=
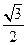，连接椭圆的四个顶点得到的菱形的面积为4.
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l与椭圆相交于不同的两点A、B，已知点A的坐标为（-a，0）.
（i）若
，求直线l的倾斜角；
（ii）若点Q
在线段AB的垂直平分线上，且
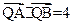.求
的值.
已知函数f（x）=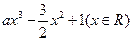
，其中a>0.
（Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；
（Ⅱ）若在区间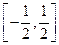
上，f（x）>0恒成立，求a的取值范围.
如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=错误!不能通过编辑域代码创建对象。，∠BAD＝∠CDA＝45°.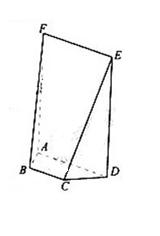
（Ⅰ）求异面直线CE与AF所成角的余弦值；
（Ⅱ）证明CD⊥平面ABF；
（Ⅲ）求二面角B-EF-A的正切值。