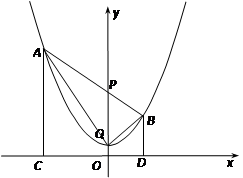（2011贵州毕节，26，12分）小明到一家批发兼零售的文具店给九年级学生购买考试用2B铅笔，请根据下列情景解决问题。
 |
售货员 小明
(1) 这个学校九年级学生总数在什么范围内？(4分)
(2) 若按批发价购买6支与按零售价购买5支的所付款相同，那么这个学校九年级学生有多少人？(8分)
已知：如图，四边形ABCD是菱形，对角线AC与BD相交于O，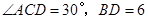
．
（1）求证：△ABD是等边三角形；
（2）求 AC的长（结果可保留根号）．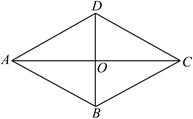 
先化简：
，再选择一个你喜欢的x值代入求值.
解不等式：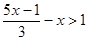
，并将解集在数轴上表示出来．
计算： 
．
如图，已知点A(−3，5)在抛物线y=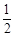
x2+c的图象上，点P从抛物线的顶点Q出发，沿y轴以
每秒1个单位的速度向正方向运动，连结AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂
足为C、D，连结AQ、BQ．
(1)求抛物线的解析式；
(2)当A、Q、B三点构成以AQ为直角边的直角三角形时，求点P离开点Q多少时间？
(3)试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）时，点P离开点Q的时刻．