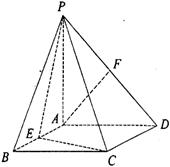
如图，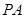
垂直于矩形
所在的平面，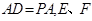
分别是
的中点.
（I）求证：
平面
；
（Ⅱ）求证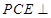：平面
平面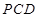
. 
已知复数
（
是虚数单位）在复平面上对应的点依次为
，点
是坐标原点.
（1）若
,求
的值；
（2）若
点的横坐标为
,求
.
已知数列
和
满足：
，其中
为实数，
为正整数.
（1）对任意实数，求证：
不成等比数列；
（2）试判断数列是否为等比数列，并证明你的结论.
（3）设
为数列的前项和.是否存在实数，使得对任意正整数，都有
?若存在，求的取值范围；若不存在，说明理由.
阅读：
已知
、
，
，求
的最小值.
解法如下：
，
当且仅当
，即
时取到等号，
则的最小值为
.
应用上述解法，求解下列问题：
（1）已知
，
，求
的最小值；
（2）已知
，求函数
的最小值；
（3）已知正数
、
、
，
，
求证：
.
如图，
、
是两个小区所在地，、到一条公路
的垂直距离分别为
，
，两端之间的距离为
.
（1）某移动公司将在之间找一点
，在处建造一个信号塔，使得对
、的张角与对
、的张角相等，试确定点的位置.
（2）环保部门将在之间找一点
，在
处建造一个垃圾处理厂，使得对、所张角最大，试确定点的位置.
已知椭圆
，
、
是椭圆的左右焦点，且椭圆经过点
.
（1）求该椭圆方程；
（2）过点
且倾斜角等于
的直线
，交椭圆于
、
两点，求
的面积.