设两个非零向量 不共线.
不共线.
(1)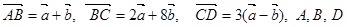 三点是否能构成三角形, 并说明理由.
三点是否能构成三角形, 并说明理由.
(2)试确定实数k, 使
(本小题12分)为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题: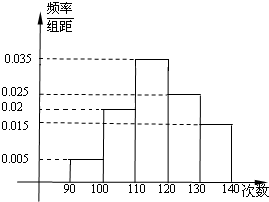
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
(本小题12分)已知 ,
, ,点
,点 的坐标为
的坐标为 .
.
(1)求当 时,点
时,点 满足
满足 的概率;
的概率;
(2)求当 时,点
时,点 满足
满足 的概率.
的概率.
命题 :关于
:关于 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 交于
交于 两点,点
两点,点 是椭圆
是椭圆 的右顶点.直线
的右顶点.直线 与直线
与直线 分别与
分别与 轴交于点
轴交于点 ,试问以线段
,试问以线段 为直径的圆是否过
为直径的圆是否过 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
(本小题共12分)如图,PA 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(1)当点E为BC的中点时, 证明EF//平面PAC;
(2)求三棱锥E-PAD的体积;
(3)证明:无论点E在边BC的何处,都有PE AF.
AF.