在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
 时,求PE及DH的长。
时,求PE及DH的长。
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.
(1)求NC,MC的长(用t的代数式表示);
(2)当t为何值时,四边形PCDQ构成平行四边形;
(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;
(4)探究:t为何值时,△PMC为等腰三角形.
已知:二次函数y=ax2+bx-2的图象经过点(1,0),一次函数图象经过原点和点(1,-b),其中a>b>0且a、b为实数.
(1)求一次函数的表达式(用含b的式子表示);
(2)试说明:这两个函数的图象交于不同的两点;
(3)设(2)中的两个交点的横坐标分别为x1、x2,求|x1-x2|的范围.
某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此太阳光线与地面成30°夹角.(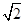 ≈1.4,
≈1.4,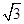 ≈1.7)
≈1.7) 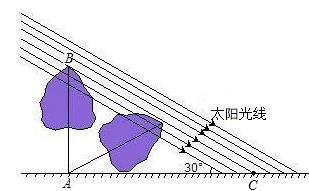
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线于地面夹角保持不变(用图(2)解答)
①求树与地面成45°角时的影长;
②求树的最大影长.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.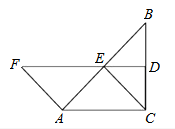
(1)说明四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
关于x的方程(k-2)x2-2(k-1)x+k+1=0,且k≤3.求证:方程总有实数根.