如图,在平行四边形ABCD中,AB在x轴上,D点y轴上,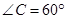 ,
, ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边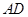 上一点,且
上一点,且 .点
.点 、
、 分别从
分别从 、
、 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿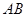 、
、 向点
向点 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为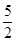 ,设运动时间为
,设运动时间为 秒。
秒。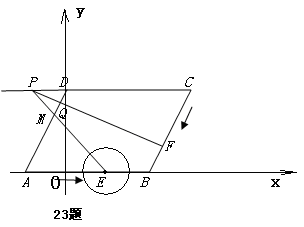
求直线BC的解析式。
当
 为何值时,
为何值时, ?
?在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。
如图,已知□ABCD中,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连结AF、CE.
(1)求证:△ADE≌△BCF;
(2)求证:四边形AECF为平行四边形;
(3)当□AECF为菱形时,M点恰为BC的中点,求CF:BC的值.
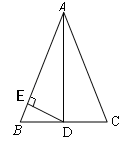
如图,BD是海秀大道东西走向的一段.海秀大道限速70千米/小时.在测速点A的正北方 米的B处有一辆汽车正向东行驶.第一次测得该汽车在A的北偏东300的C处;2秒钟后,又测得该汽车在A的北偏东600的D处.求这辆汽车的速度是多少?它超速了吗?
米的B处有一辆汽车正向东行驶.第一次测得该汽车在A的北偏东300的C处;2秒钟后,又测得该汽车在A的北偏东600的D处.求这辆汽车的速度是多少?它超速了吗? 
某城市对教师试卷讲评课中学生参与的深度与广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图(图1,图2),请根据图中所给信息解答下列问题: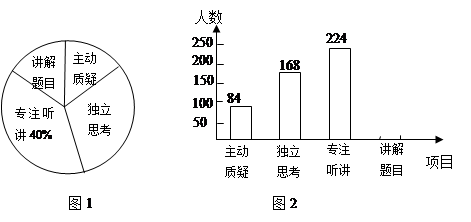
(1)在这次评价中,一共抽查了名学生;
(2)请将条形图补充完整;
(3)在扇形统计图中,“主动质疑”所对应的扇形圆心角度数为;
(4)如果全市有16万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人?
某宾馆有单人间和双人间两种房间,入住3个单人间和6个双人间共需1020元,入住1个单人间和5个双人间共需700元,则入住单人间和双人间各5个共需多少元?
如图,在△ABC中,AB=AC=13,BC=10,AD⊥BC于点D,DE⊥AB于点E,则BE等于.