计算: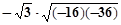 ;
;
如图,抛物线y=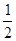 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).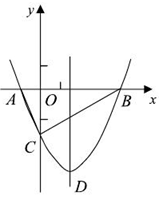
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
已知二次函数y=-x2+4x+5,完成下列各题:
(1)将函数关系式用配方法化为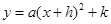 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
(2)求出它的图象与坐标轴的交点坐标.
(3)在直角坐标系中,画出它的图象.
(4)根据图象说明:当x为何值时,y>0;当x为何值时,y<0.
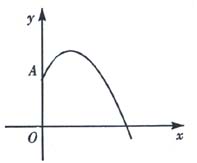
如图,某学生推铅球,铅球出手(点A处)的高度是0.6m,出手后的铅球沿一段抛物线运行,当运行到最高3m时,水平距离x=4m.
(1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?