已知函数 的图象与
的图象与 在原点相切,且函数的极小值为
在原点相切,且函数的极小值为 ,(1)求
,(1)求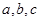 的值;(2)求函数的递减区间.
的值;(2)求函数的递减区间.
已知直三棱柱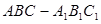 中,
中, 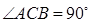 ,
,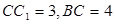 ,
, 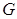 是
是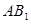 和
和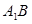 的交点, 若
的交点, 若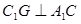 .
.
(1)求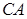 的长;(2)求点
的长;(2)求点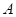 到平面
到平面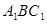 的距离;
的距离;
(3)求二面角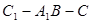 的平面角的正弦值的大小.
的平面角的正弦值的大小.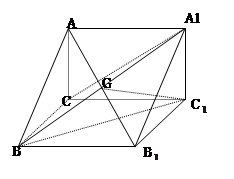
把函数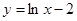 的图象按向量
的图象按向量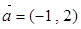 平移得到函数
平移得到函数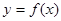 的图象.
的图象.
(1)求函数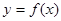 的解析式; (2)若
的解析式; (2)若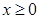 ,证明:
,证明: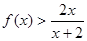 .
.
求由抛物线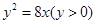 与直线
与直线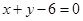 及
及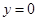 所围成图形的面积.
所围成图形的面积.
求圆心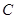 在直线
在直线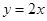 上,且经过原点及点
上,且经过原点及点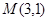 的圆
的圆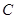 的标准方程.
的标准方程.
已知函数f(x)(x∈R)满足f(x)=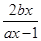 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1=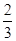 ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).