(本小题满分14分) 已知数列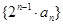 的前n项和Sn=9-6n.
的前n项和Sn=9-6n.
(1)求数列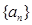 的通项公式.
的通项公式.
(2)设 ,求数列
,求数列 的前n项和.
的前n项和.
(本小题满分12分)已知 ,
,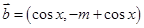 ,且
,且
(1)求函数 的解析式;
的解析式;
(2)当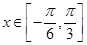 时,
时, 的最小值是
的最小值是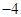 ,求此时函数
,求此时函数 的最大值,并求出函数
的最大值,并求出函数 取得最大值时自变量
取得最大值时自变量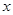 的值
的值
(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组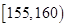 、第二组
、第二组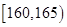 ;…第八组
;…第八组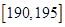 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第六组比第七组多1人,第一组和第八组人数相同.
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第六组比第七组多1人,第一组和第八组人数相同.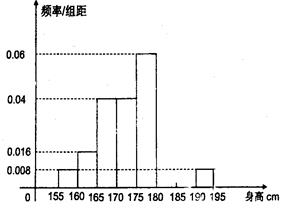
(Ⅰ)求第六组、第七组的频率并补充完整频率分布直方图;
(Ⅱ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为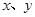 ,求满足
,求满足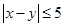 的事件概率;
的事件概率;
(本小题满分12分)已知 ,
,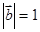 ,
, .
.
(Ⅰ)求向量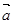 与
与 的夹角θ;
的夹角θ;
(Ⅱ)求 及向量
及向量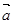 在
在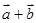 方向上的投影.
方向上的投影.
(本小题满分12分)已知: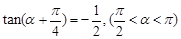 。
。
(1)求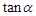 的值;
的值;
(2)求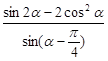 的值。
的值。
已知数列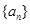 满足
满足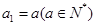 .
.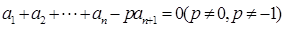
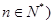 .
.
(1)数列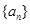 的通项公式;
的通项公式;
(2)对每一个正整数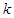 ,若将
,若将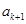 ,
,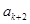 ,
,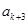 按从小到大的顺序排列后,此三项均能构成等差数列,且记公差为
按从小到大的顺序排列后,此三项均能构成等差数列,且记公差为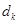 .求
.求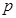 的值及相应的数列
的值及相应的数列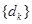 ;
;