(本小题满分12分)在直三棱柱ABC—A1B1C1中,∠ ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、
ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、 BC的中点,M为棱AA1上的点。
BC的中点,M为棱AA1上的点。
(1)证明:A1B1⊥C1D;
(2)当 的大小。
的大小。
设a为实数,函数 ,
, .
.
(1)求 的单调区间及极值;
的单调区间及极值;
(2)求证:当 且
且 时,
时, .
.
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:
(Ⅰ)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入下表.
抽取人数 6
(Ⅰ)在(Ⅰ)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
设函数 ,其中
,其中 .已知
.已知 在
在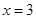 处取得极值.
处取得极值.
(1)求 的解析式;
的解析式;
(2)求 在点
在点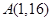 处的切线方程.
处的切线方程.
已知函数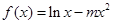 ,
,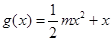 (
( ),令
),令 .
.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若关于x的不等式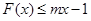 恒成立,求整数m的最小值.
恒成立,求整数m的最小值.
设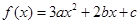 ,若
,若 ,
,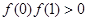 ,求证:
,求证:
(Ⅰ)方程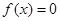 有实根.
有实根.
(Ⅱ) ;设x1,x2是方程
;设x1,x2是方程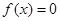 的两个实根,则
的两个实根,则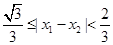 .
.