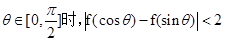(本小题满分12分)
已知函数 的图象与x轴的交点中,相邻两个交点之间的距离为
的图象与x轴的交点中,相邻两个交点之间的距离为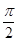 ,且图象上一个最低点为
,且图象上一个最低点为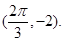
(I)求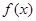 的解析式;
的解析式;
(II)当 的值域。
的值域。
已知函数
(1)讨论函数f (x)的极值情况;
(2)设g (x) =" ln(x" + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
如图所示,在直三棱柱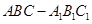 中,
中,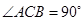 ,
,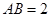 ,
,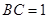 ,
,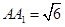 ,点
,点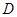 是棱
是棱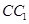 的中点.
的中点.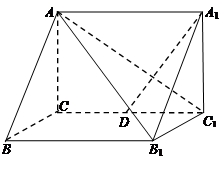
(Ⅰ)证明:平面AA1C1C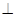 平面
平面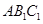 ;
;
(Ⅱ)求二面角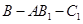 的余弦值.
的余弦值.
设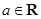 ,函数
,函数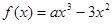
(Ⅰ)若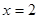 是函数
是函数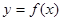 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若函数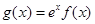 在
在 上是单调减函数,求实数
上是单调减函数,求实数 的取值范围.
的取值范围.
已知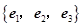 为空间的一个基底,且
为空间的一个基底,且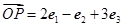 ,
, 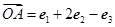 ,
,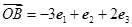 ,
,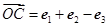
(1)判断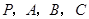 四点是否共面;
四点是否共面;
(2)能否以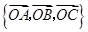 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量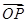
设 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(Ⅰ)求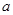 的值,并讨论
的值,并讨论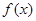 的单调性;
的单调性;
(Ⅱ)证明:当