(本小题满分12分)
已知函数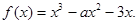
(I)若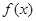 在区间
在区间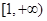 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(II)若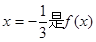 的一个极值点,求
的一个极值点,求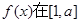 上的最大值;
上的最大值;
(III)在(II)的条件下,是否存在实数b,使得函数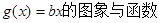
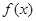 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由。
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由。
(本小题满分14分)已知抛物线
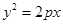 (
(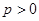 )过点
)过点 .
.
(1)求抛物线 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线焦点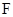 的直线
的直线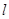 与抛物线
与抛物线 相交于两点
相交于两点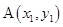 、
、 ,点
,点 在抛物线
在抛物线 的准线上,
的准线上,
且满足直线 平行
平行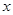 轴,试判断坐标原点
轴,试判断坐标原点 与直线
与直线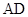 的关系,并证明你的结论.
的关系,并证明你的结论.
(本小题满分14分)已知数列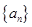 的前
的前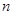 项和
项和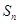 与
与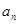 满足
满足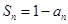 (
( ).
).
(1)求数列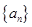 的通项公式;
的通项公式;
(2)求数列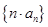 的前
的前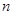 项和
项和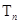 .
.
(本小题满分14分)如图,在四棱锥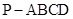 中,
中,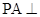 平面
平面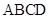 ,
,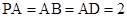 ,
,
四边形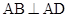 ,
,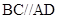 且
且 ,点
,点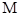 为
为 中点.
中点.
(1)求证:平面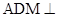 平面
平面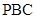 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)从一批草莓中,随机抽取 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
| 分组(重量) |
 |
 |
 |
 |
| 频数(个) |
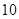 |
 |
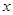 |
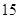 |
已知从 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在 的草莓的概率为
的草莓的概率为 .
.
(1)求出 ,
,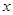 的值;
的值;
(2)用分层抽样的方法从重量在 和
和 的草莓中共抽取
的草莓中共抽取 个,再从这
个,再从这 个草莓中任取
个草莓中任取 个,
个,
求重量在 和
和 中各有
中各有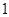 个的概率.
个的概率.
【原创】(本小题满分12分)已知函数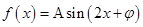 (
(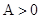 ,
, ),
), 的最大值是
的最大值是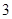 ,其图象经过点
,其图象经过点 .
.
(1)求函数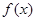 的解析式;
的解析式;
(2)若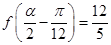 ,求
,求 的值.
的值.