如图,把Rt△ACB与Rt△DCE按图(甲)所示重叠在一起,其中AC="2," ∠BAC=60°,若把Rt△DCE绕直角 顶点C按顺时针方向旋转30°,使得A B分别与DC, DE相交于点F、G, CB与DE相交于点M,如图(乙)所示.
顶点C按顺时针方向旋转30°,使得A B分别与DC, DE相交于点F、G, CB与DE相交于点M,如图(乙)所示.求CM的长;
求△ACB与△DCE的重叠部分(即四边形CMGF)的面积(保留根号)
将△DCE按顺时针方向继续旋转45°,得△
 C
C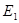 ,这时,点
,这时,点 在△ACB的内部,外部,还是边上?证明你的判断.
在△ACB的内部,外部,还是边上?证明你的判断.
如图,已知 为
为 的直径,
的直径, 是
是 的切线,
的切线, 为切点,
为切点,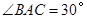
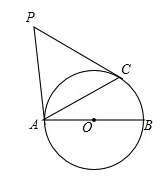
(Ⅰ)求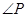 的大小;
的大小;
(Ⅱ)若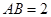 ,求
,求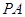 的长(结果保留根号).
的长(结果保留根号).
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.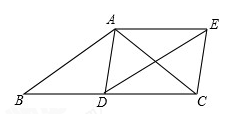
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
在等腰△ABC中,三边分别为a、b、c,其中a=5,若关于x的方程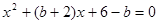 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
(1)x2+2x=1
(2)x(x﹣3)=x﹣3
如图所示,菱形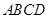 的顶点
的顶点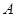 、
、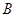 在
在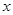 轴上,点
轴上,点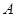 在点
在点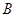
的左侧,点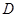 在
在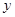 轴的正半轴上,
轴的正半轴上,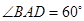 ,点
,点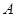 的坐标为(-2,0).
的坐标为(-2,0). 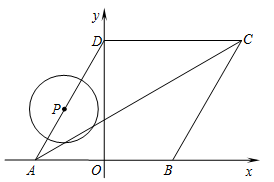
(1)求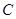 点的坐标;
点的坐标;
(2)求直线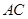 的函数关系式;
的函数关系式;
(3)动点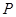 从点
从点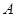 出发,以每秒1个单位长度的速度,按照
出发,以每秒1个单位长度的速度,按照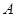 →
→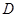 →
→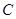 →
→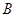 →
→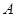 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为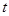 秒.求
秒.求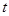 为何值时,以点
为何值时,以点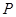 为圆心、以1为半径的圆与对角线
为圆心、以1为半径的圆与对角线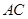 相切?
相切?