已知数列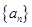 的前
的前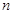 项和为
项和为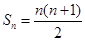 .
.
(Ⅰ)求数列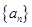 的通项公式
的通项公式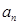 ;
;
(Ⅱ)记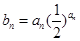 ,求数列
,求数列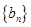 的前
的前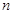 项和
项和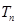
某人上楼梯,每步上一阶的概率为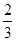 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第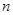 阶的概率为
阶的概率为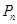 .
.
(1)求 ;;
;;
(2)该人共走了5步,求该人这5步共上的阶数ξ的数学期望.
设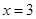 是函数
是函数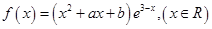 的一个极值点。
的一个极值点。
(1)求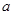 与
与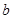 的关系式(用
的关系式(用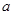 表示
表示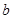 ),并求
),并求 的单调区间;
的单调区间;
(2)设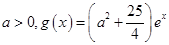 ,若存在
,若存在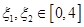 ,使得
,使得 成立,求实数
成立,求实数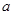 的取值范围。
的取值范围。
过点 的直线
的直线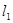 交直线
交直线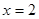 于
于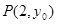 ,过点
,过点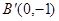 的直线
的直线 交
交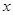 轴于
轴于 点,
点, ,
, .
.
(1)求动点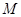 的轨迹
的轨迹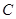 的方程;
的方程;
(2)设直线l与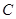 相交于不同的两点
相交于不同的两点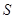 、
、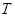 ,已知点
,已知点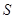 的坐标为(-2,0),点Q(0,
的坐标为(-2,0),点Q(0, )在线段
)在线段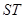 的垂直平分线上且
的垂直平分线上且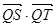 ≤4,求实数
≤4,求实数 的取值范围.
的取值范围.
已知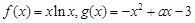 .
.
(1)已知函数h(x)=g(x)+ax3的一个极值点为1,求a的取值;
(2) 求函数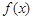 在
在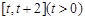 上的最小值;
上的最小值;
(3)对一切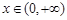 ,
,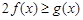 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知函数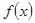 是定义在
是定义在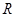 上的偶函数,且当
上的偶函数,且当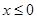 时,
时,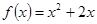 .现已画出函数
.现已画出函数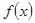 在
在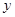 轴左侧的图像,如图所示,并根据图像
轴左侧的图像,如图所示,并根据图像
(1)写出函数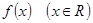 的增区间;
的增区间;
(2)写出函数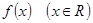 的解析式;
的解析式;
(3)若函数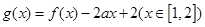 ,求函数
,求函数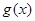 的最小值。
的最小值。