对于给定数列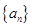 ,如果存在实常数
,如果存在实常数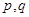 ,使得
,使得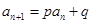 对于任意
对于任意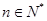 都成立,我们称数列
都成立,我们称数列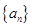 是 “
是 “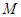 类数列”.
类数列”.
(Ⅰ)已知数列 是 “
是 “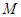 类数列”且
类数列”且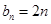 ,求它对应的实常数
,求它对应的实常数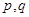 的值;
的值;
(Ⅱ)若数列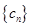 满足
满足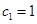 ,
,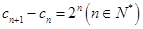 ,求数列
,求数列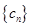 的通项公式.并判断
的通项公式.并判断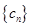 是否为“
是否为“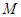 类数列”,说明理由.
类数列”,说明理由.
已知动圆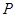 与圆
与圆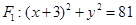 相切,且与圆
相切,且与圆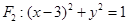 相内切,记圆心
相内切,记圆心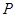 的轨迹为曲线
的轨迹为曲线 ;设
;设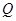 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点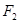 作
作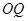 的平行线交曲线
的平行线交曲线 于
于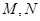 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究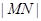 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记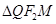 的面积为
的面积为 ,
, 的面积为
的面积为 ,令
,令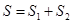 ,求
,求 的最大值.
的最大值.
已知数列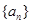 中,
中,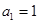 ,
,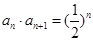 ,记
,记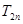 为
为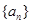 的前
的前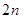 项的和,
项的和,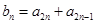 ,
,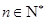 .
.
(1)判断数列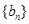 是否为等比数列,并求出
是否为等比数列,并求出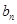 ;
;
(2)求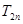 .
.
如图,在四棱锥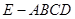 中,底面
中,底面 为正方形,
为正方形,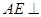 平面
平面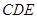 ,已知
,已知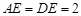 ,
,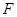 为线段
为线段 的中点.
的中点.
(1)求证: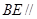 平面
平面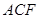 ;
;
(2)求二面角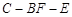 的平面角的余弦值.
的平面角的余弦值.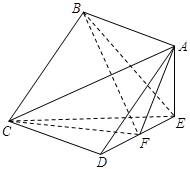
某大型公益活动从一所名牌大学的四个学院中选出了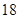 名学生作为志愿者,参加相关的活
名学生作为志愿者,参加相关的活
动事宜.学生来源人数如下表:
| 学院 |
外语学院 |
生命科学学院 |
化工学院 |
艺术学院 |
| 人数 |
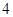 |
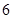 |
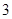 |
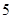 |
(1)若从这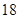 名学生中随机选出两名,求两名学生来自同一学院的概率;
名学生中随机选出两名,求两名学生来自同一学院的概率;
(2)现要从这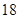 名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为
名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为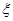 ,令
,令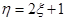 ,求随机变量
,求随机变量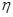 的分布列及数学期望
的分布列及数学期望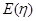 .
.
已知函数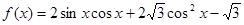 ,
,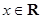 .
.
(1)求函数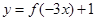 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)已知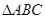 中的三个内角
中的三个内角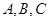 所对的边分别为
所对的边分别为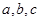 ,若锐角
,若锐角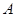 满足
满足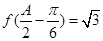 ,且
,且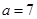 ,
,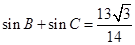 ,求
,求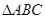 的面积.
的面积.