为了更好地治理洋澜湖水质，保护环境，市治污公司决定购买10台，污水处理设备，现有A，B两种型号的设备，其中每台的价格，同处理污水量如下表：
| |
A型 |
B型 |
| 价格（万元/台） |
a |
b |
| 处理污水量（吨/月） |
240 |
200 |
经调查：购买一台A型号设备比购买一台B型号设备多2万元，购买2台A型设备比购买3台B型号设备少6万元。求a ，b的值
经预算：使治污公司购买污水处理设备的资金不超过105万元，若每月要求处理洋澜湖的污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案。
如图, 已知A（－4，－1），B（－5，－4），C（－1，－3），△ABC经过平移得到的△A′B′C′,△ABC中任意一点P（x1,y1）平移后的对应点为P′（x1+6,y1+4）。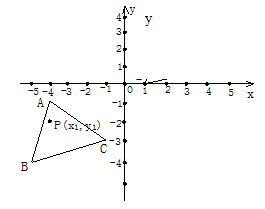
（1）请在图中作出△A′B′C′；
（2）写出点A′、B′、C′的坐标.
已知关于x、y的方程组满足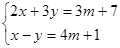
且它的解是一对正数
（1）试用m表示方程组的解；（2）求m的取值范围；
（3）化简
。
解方程组或不等式组
（1）
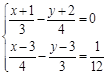（2）
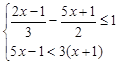
如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运费15 000元，铁路运费97 200元，请计算这批产品的销售款比原料费和运输费的和多多少元？
（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲：
乙：
根据甲，乙两名同学所列方程组，请你分别指出未知数x，y表示的意义，然后在等式右边的方框内补全甲、乙两名同学所列方程组．
甲：x表示 ，y表示
乙：x表示 ，y表示
（2）甲同学根据他所列方程组解得x=300，请你帮他解出y的值，并解决该实际问题．
如图，AD=CD，AC平分∠DAB，求证：DC∥AB．