已知过抛物线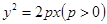 的焦点,斜率为
的焦点,斜率为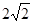 的直线交抛物线于
的直线交抛物线于
 (
( )两点,且
)两点,且 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点,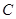 为抛物线上一点,若
为抛物线上一点,若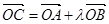 ,求
,求 的值.
的值.
在直角坐标系xOy中,直线l的参数方程为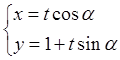 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(1)求直线l与曲线C的平面直角坐标方程;
(2)设直线l与曲线C交于不同的两点A、B,若 ,求α的值.
,求α的值.
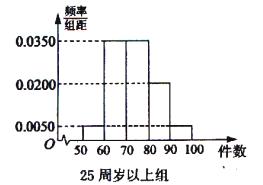
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组: 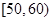 ,
,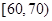 ,
,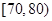 ,
,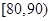 ,
,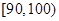 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成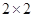 的列联表,并判断是否有
的列联表,并判断是否有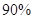 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?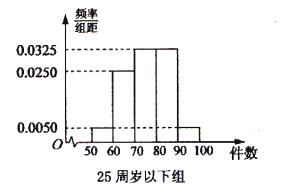
附表:
某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为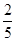 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为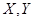 ,求
,求 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
某车间共有 名工人,随机抽取
名工人,随机抽取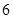 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 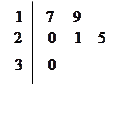
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间 名工人中,任取
名工人中,任取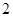 人,求恰有
人,求恰有 名优秀工人的概率.
名优秀工人的概率.
按照下列要求,分别求有多少种不同的方法?
(1)6个不同的小球放入4个不同的盒子;
(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;
(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球;
(4)6个不同的小球放入4个不同的盒子,恰有1个空盒.