如图是一个几何体的三视图,其中正视图与左视图都是全等的腰为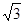 的等腰三角形,俯视图是边长为2的正方形,(1)画出该几何体;(2)求此几何体的表面积与体积.
的等腰三角形,俯视图是边长为2的正方形,(1)画出该几何体;(2)求此几何体的表面积与体积.
已知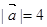 ,
,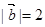 ,且
,且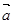 与
与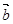 夹角为120°求:
夹角为120°求:
(1)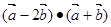 ;
;
(2)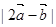 ;
;
(3)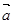 与
与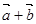 的夹角。
的夹角。
对定义在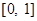 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数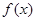 称为
称为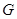 函数.
函数.
①对任意的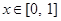 ,总有
,总有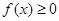 ;
;
②当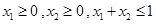 时,总有
时,总有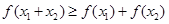 成立.
成立.
已知函数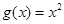 与
与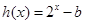 是定义在
是定义在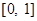 上的函数.
上的函数.
(1)试问函数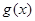 是否为
是否为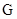 函数?并说明理由;
函数?并说明理由;
(2)若函数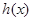 是
是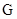 函数,求实数
函数,求实数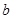 组成的集合.
组成的集合.
设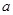 是实数,
是实数,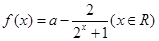 ,
,
(1)已知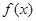 是奇函数,求
是奇函数,求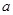 ;
;
(2)用定义证明:对于任意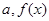 在
在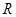 上为增函数.
上为增函数.
已知函数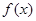 的定义域是(0,+∞),且满足
的定义域是(0,+∞),且满足 ,
,  ,如果对于
,如果对于 ,都有
,都有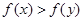 .
.
(1)求 的值;
的值;
(2)解不等式 .
.