（本小题14分）如图所示，L是海面上一条南北方向的海防警戒线，在L上点A处有一个水声监测点，另两个监测点B，C分别在A的正东方20 km处和54 km处．某时刻，监测点B收到发自静止目标P的一个声波，8s后监测点A，20 s后监测点C相继收到这一信号．在当时气象条件下，声波在水中的传播速度是1. 5 km/s.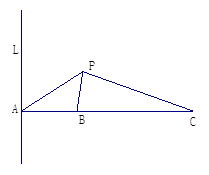
（1）设A到P的距离为
km，用分别表示B、C到P 的距离，并求值；
（2）求静止目标P到海防警戒线L的距离（结果精确到0.01 km）
（本小题满分12分）设函数
，若
（1）求函数
的解析式；
（2）画出函数的图象，并指出函数的定义域、值域、单调区间．
（本小题满分11分）
（1）计算
（2）计算
（本小题满分11分）已知全集为
，集合
，
,
（1）求
；（2）求
；（3）若
，求
的取值范围．
（本小题满分10分）如图甲，⊙
的直径
，圆上两点
在直径
的两侧，使
， 
．沿直径折起，使两个半圆所在的平面互相垂直（如图乙），
为
的中点．根据图乙解答下列各题：
（1）求点
到平面
的距离；
（2）如图:若
的平分线交弧
于一点
,试判断
是否与平面
平行？并说明理由．
（本小题满分12分）已知以点C
（t∈R，t≠0）为圆心的圆与x轴交于点O、A两点，与y轴交于点O，B，其中O为原点．
（1）求证：△AOB的面积为定值；
（2）设直线2x＋y－4＝0与圆C交于点M，N，若
，求圆C的方程；
（3）在（2）的条件下，设P，Q分别是直线l：x＋y＋2＝0和圆C上的动点，求
的最小值及此时点P的坐标．