已知函数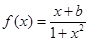 为奇函数。
为奇函数。
(I)证明:函数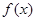 在区间(1,
在区间(1, )上是减函数;
)上是减函数;
(II)解关于x的不等式
动点P到定点D(1,0)的距离与到直线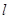 :
: 的距离相等,动点P形成曲线记作C。
的距离相等,动点P形成曲线记作C。
(1)求动点P的轨迹方程
(2)过点Q(4,1)作曲线C的弦AB,恰被Q平分,求AB所在直线方程.
如图,四棱锥P—ABCD的底面为菱形且 ,PA⊥底面ABCD,AB=2
,PA⊥底面ABCD,AB=2 ,PA=
,PA= ,E为PC的中点。
,E为PC的中点。
(1)求直线DE与平面PAC所成角的大小;
(2)求二面角E—AD—C的余弦值。
如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
, ,平面
,平面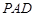 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点,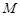 是棱
是棱 上的点,
上的点,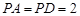 ,
,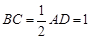 ,
,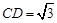 .
.
(Ⅰ)求证:平面 ⊥平面
⊥平面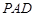 ;
;
(Ⅱ)若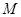 为棱
为棱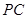 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
直线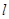 过点P(0,2)且与椭圆
过点P(0,2)且与椭圆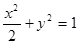 相交于M,N两点,求
相交于M,N两点,求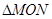 面积的最大值。
面积的最大值。
已知抛物线 与直线
与直线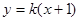 相交于A,B两点。
相交于A,B两点。
(1)求证:OA⊥OB;
(2)当 的面积等于
的面积等于 时,求
时,求 的值。
的值。