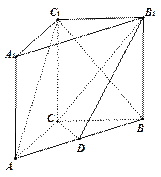
已知三棱柱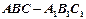 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图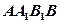 和侧视图
和侧视图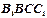 均为矩形,俯视图
均为矩形,俯视图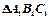 中,
中,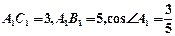 。
。
(I)在三棱柱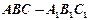 中,求证:
中,求证: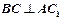 ;
;
(II)在三棱柱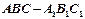 中,若
中,若 是底边
是底边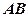 的中点,求证:
的中点,求证: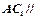 平面
平面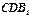 ;
;
(10分)已知圆C与圆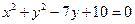 相交,所得公共弦平行于已知直线
相交,所得公共弦平行于已知直线 ,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
(10分)△ABC中,已知三个顶点的坐标分别是A(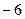 ,0),B(6,0),C(6,5),
,0),B(6,0),C(6,5),
(1)求AC边上的高线BH所在的直线方程;
(2)求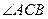 的角平分线所在直线的方程。
的角平分线所在直线的方程。
(本小题满分12分)设递增等比数列{ }的前n项和为
}的前n项和为 ,且
,且 =3,
=3, =13,数列{
=13,数列{ }满足
}满足
 =
= ,点P(
,点P( ,
, )在直线x-y+2=0上,n∈N﹡
)在直线x-y+2=0上,n∈N﹡
(Ⅰ)求数列{
 },{
},{ }的通项公式
}的通项公式
(Ⅱ)设 =
= ,数列{
,数列{ }的前n项和
}的前n项和 ,若
,若 >2a-1恒成立(n∈N﹡),求实数a的取值范围.
>2a-1恒成立(n∈N﹡),求实数a的取值范围.
(本小题满分12分)
已知半圆x2+y2=3(y≥0),P为半圆上任一点,A(2,0)为定点,以P A为边作正三角形PAB,且点B与圆心分别在PA的两侧,求四边形POAB面积的最大值.
A为边作正三角形PAB,且点B与圆心分别在PA的两侧,求四边形POAB面积的最大值.