某产品按行业生产标准分成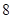个等级，等级系数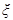依次为，其中为标准，-优题课

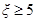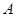某产品按行业生产标准分成个等级，等级系数依次为，其中为标准，为标准，产品的等级系数越大表明产品的质量越好. 已知某厂执行标准生产该产品，且该厂的产品都符合相应的执行标准．从该厂生产的产品中随机抽取件，相应的等级系数组成一个样本，数据如下：
3   5   3   3   8   5   5   6   3   4
6   3   4   7   5   3   4   8   5   3
8   3   4   3   4   4   7   5   6   7
该行业规定产品的等级系数的为一等品，等级系数的为二等品，等级系数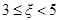的为三等品．
（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率；
（2）从样本的一等品中随机抽取2件，求所抽得2件产品等级系数都是8的概率